化简 ,下列结果中,正确的是( )
A . B .
C . 2 D . -2
下列图形中,既是轴对称图形又是中心对称图形的是( )
A . ![]() B .
B . ![]() C .
C . ![]() D .
D . ![]()
下列计算中,结果正确的是( )
A . B .
C .
D .
下列图形中,正方体展开图错误的是( )
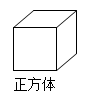
A . 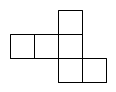 B .
B . 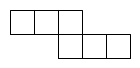 C .
C . 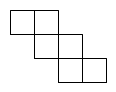 D .
D . 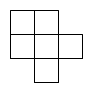
若式子 在实数范围内有意义,则 x 的取值范围是( )
A . B .
C .
且
D .
且
下列命题中是假命题的是( )
A .三角形的中位线平行于三角形的第三边,并且等于第三边的一半
B .如果两个角互为邻补角,那么这两个角一定相等
C .从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角
D .直角三角形斜边上的中线等于斜边的一半
如图,线段 在平面直角坐标系内, A 点坐标为
,线段
绕原点 O 逆时针旋转 90° ,得到线段
,则点
的坐标为( )
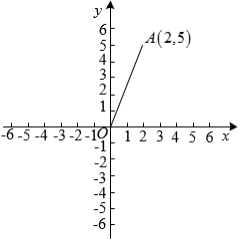
A . B .
C .
D .
学校组织学生进行知识竞赛, 5 名参赛选手的得分分别为: 96 , 97 , 98 , 96 , 98. 下列说法中正确的是( )
A .该组数据的中位数为 98 B .该组数据的方差为 0.7
C .该组数据的平均数为 98 D .该组数据的众数为 96 和 98
有一个容积为 24 的圆柱形的空油罐,用一根细油管向油罐内注油,当注油量达到该油罐容积的一半时,改用一根口径为细油管口径 2 倍的粗油管向油罐注油,直至注满,注满油的全过程共用 30 分钟,设细油管的注油速度为每分钟 x
,由题意列方程,正确的是( )
A . B .
C .
D .
已知二次函数 的部分函数图象如图所示,则一次函数
与反比例函数
在同一平面直角坐标系中的图象大致是( )

A . 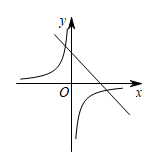 B .
B . 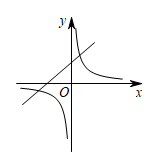
C . 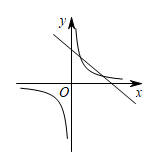 D .
D . 
小王同学从家出发,步行到离家 a 米的公园晨练, 4 分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离 y (单位:米)与出发时间 x (单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
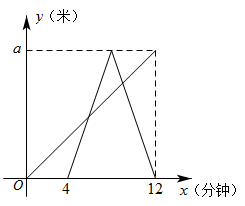
A . 2.7 分钟 B . 2.8 分钟 C . 3 分钟 D . 3.2 分钟
如图,在矩形 中, P 是边
上的一个动点,连接
,
,过点 B 作射线,交线段
的延长线于点 E ,交边
于点 M ,且使得
,如果
,
,
,
,其中
.则下列结论中,正确的个数为( )
( 1 ) y 与 x 的关系式为 ;( 2 )当
时,
;( 3 )当
时,
.

A . 0 个 B . 1 个 C . 2 个 D . 3 个
一个不透明的箱子中有 5 个红球和若干个黄球,除颜色外无其它差别 . 若任意摸出一个球,摸出红球的概率为 ,则这个箱子中黄球的个数为 个.
因式分解: .
不等式组 的解集为
,则 m 的取值范围为 .
已知圆锥的高为 8 ,母线长为 10
,则其侧面展开图的面积为 .
设 与
为一元二次方程
的两根,则
的值为 .
定义一种运算; ,
.例如:当
,
时,
,则
的值为 .
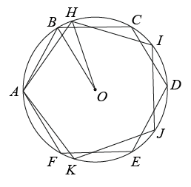
如图,正六边形 和正五边形
内接于
,且有公共顶点 A ,则
的度数为 度.
某班为奖励在数学竞赛中成绩优异的同学,花费 48 元钱购买了甲、乙两种奖品,每种奖品至少购买 1 件,其中甲种奖品每件 4 元,乙种奖品每件 3 元,则有 种购买方案.
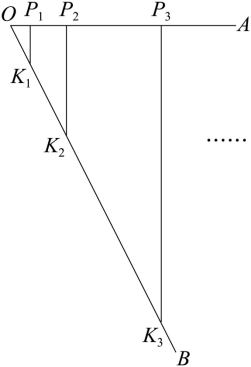
如图, ,点
在射线
上,且
,过点
作
交射线
于
,在射线
上截取
,使
;过点
作
交射线
于
,在射线
上截取
,使
. 按照此规律,线段
的长为 .
在长为 2 ,宽为 x ( )的矩形纸片上,从它的一侧,剪去一个以矩形纸片宽为边长的正方形(第一次操作);从剩下的矩形纸片一侧再剪去一个以宽为边长的正方形(第二次操作);按此方式,如果第三次操作后,剩下的纸片恰为正方形,则 x 的值为 .
已知: .
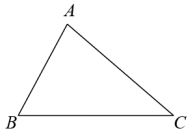
(1) 尺规作图:用直尺和圆规作出 内切圆的圆心 O ;(只保留作图痕迹,不写作法和证明)
(2) 如果 的周长为 14
,内切圆的半径为 1.3
,求
的面积.
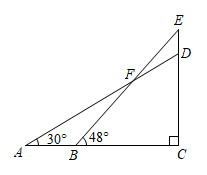
如图所示,为了测量百货大楼 顶部广告牌
的高度,在距离百货大楼 30m 的 A 处用仪器测得
;向百货大楼的方向走 10 m ,到达 B 处时,测得
,仪器高度忽略不计,求广告牌
的高度.(结果保留小数点后一位)
(参考数据: ,
,
,
)
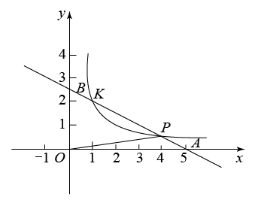
在平面直角坐标系中,已知一次函数 与坐标轴分别交于
,
两点,且与反比例函数
的图象在第一象限内交于 P , K 两点,连接
,
的面积为
.
(1) 求一次函数与反比例函数的解析式;
(2) 当 时,求 x 的取值范围;
(3) 若 C 为线段 上的一个动点,当
最小时,求
的面积.
我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题.

(1) 如图一,在等腰 中,
,
边上有一点 D ,过点 D 作
于 E ,
于 F ,过点 C 作
于 G . 利用面积证明:
.
(2) 如图二,将矩形 沿着
折叠,使点 A 与点 C 重合,点 B 落在
处,点 G 为折痕
上一点,过点 G 作
于 M ,
于 N . 若
,
,求
的长.
(3) 如图三,在四边形 中, E 为线段
上的一点,
,
,连接
,且
,
,
,
,求
的长.
如图所示,在 的内接
中,
,
,作
于点 P ,交
于另一点 B , C 是
上的一个动点(不与 A , M 重合),射线
交线段
的延长线于点 D ,分别连接
和
,
交
于点 E .
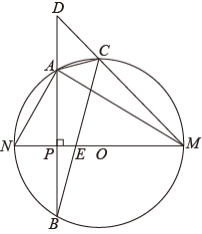
(1) 求证: .
(2) 若 ,
,求
的长.
(3) 在点 C 运动过程中,当 时,求
的值.
如图,抛物线 交 y 轴于点
,并经过点
,过点 A 作
轴交抛物线于点 B ,抛物线的对称轴为直线
, D 点的坐标为
,连接
,
,
. 点 E 从 A 点出发,以每秒
个单位长度的速度沿着射线
运动,设点 E 的运动时间为 m 秒,过点 E 作
于 F ,以
为对角线作正方形
.

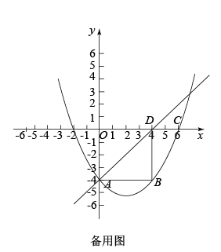
(1) 求抛物线的解析式;
(2) 当点 G 随着 E 点运动到达 上时,求此时 m 的值和点 G 的坐标;
(3) 在运动的过程中,是否存在以 B , G , C 和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点 G 的坐标,如果不存在,请说明理由.