2022 的相反数是（ ）

A ． 2022 B ． C ． D ．

若二次根式 有意义，则实数 的取值范围是（ ）

A ． B ． C ． D ．

下列图形中，为圆柱的侧面展开图的是（ ）

A ． B ．

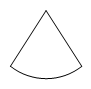C ． D ．

如图，在 △ ABC 中， D ， E 分别是 AB ， AC 边的中点，若 DE ＝ 2 ，则 BC 的长度是（　　）

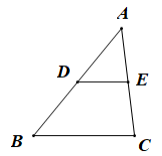
A ． 6 B ． 5

C ． 4 D ． 3

某城市市区人口 万人，市区绿地面积 50 万平方米，平均每人拥有绿地 平方米，则 与 之间的函数表达式为（ ）

A ． B ． C ． D ．

如图，斑马线的作用是为了引导行人安全地通过马路．小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一想法体现的数学依据是（ ）

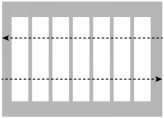
A ．垂线段最短

B ．两点确定一条直线

C ．过一点有且只有一条直线与已知直线垂直

D ．过直线外一点有且只有一条直线与已知直线平行

在平面直角坐标系 中，点 A 与点 关于 轴对称，点 A 与点 关于 轴对称．已知点 ，则点 的坐标是（ ）

A ． B ． C ． D ．

某汽车评测机构对市面上多款新能源汽车的 的加速时间和满电续航里程进行了性能评测，评测结果绘制如下，每个点都对应一款新能源汽车的评测数据．已知 的加速时间的中位数是 ，满电续航里程的中位数是 ，相应的直线将平面分成了 ① 、 ② 、 ③ 、 ④ 四个区域（直线不属于任何区域）．欲将最新上市的两款新能源汽车的评测数据对应的点绘制到平面内，若以上两组数据的中位数均保持不变，则这两个点可能分别落在（ ）

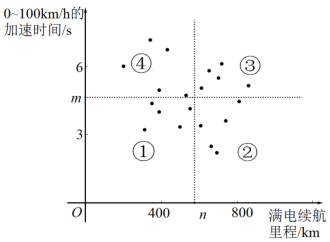
A ．区域 ① 、 ② B ．区域 ① 、 ③ C ．区域 ① 、 ④ D ．区域 ③ 、 ④

计算： =___ ．

计算： _____ ．

分解因式： ______ ．

2022 年 5 月 22 日，中国科学院生物多样性委员会发布《中国生物物种名录》 2022 版，共收录物种及种下单元约 138000 个．数据 138000 用科学记数法表示为 ______ ．

如图，数轴上的点 、 分别表示实数 、 ，则 ______ ．（填 “>” 、 “=” 或 “<” ）

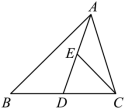
如图，在 中， 是中线 的中点．若 的面积是 1 ，则 的面积是 ______ ．

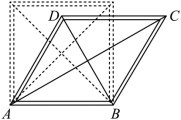
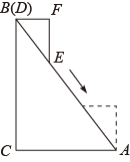
如图，将一个边长为 的正方形活动框架（边框粗细忽略不计）扭动成四边形 ，对角线是两根橡皮筋，其拉伸长度达到 时才会断裂．若 ，则橡皮筋 _____ 断裂（填 “ 会 ” 或 “ 不会 ” ，参考数据： ）．

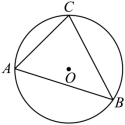
如图， 是 的内接三角形．若 ， ，则 的半径是 ______ ．

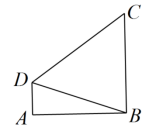
如图，在四边形 中， ， 平分 ．若 ， ，则 ______ ．

如图，在 中， ， ， ．在 中， ， ， ．用一条始终绷直的弹性染色线连接 ， 从起始位置（点 与点 重合）平移至终止位置（点 与点 重合），且斜边 始终在线段 上，则 的 外部 被染色的区域面积是 ______ ．

计算：

(1) ；

(2) ．

解不等式组 ，并把解集在数轴上表示出来．

为减少传统塑料袋对生态环境的破坏，国家提倡使用可以在自然环境下（特定微生物、温度、湿度）较快完成降解的环保塑料袋．调查小组就某小区每户家庭 1 周内环保塑料袋的使用情况进行了抽样调查，使用情况为 （不使用）、 （ 1~3 个）、 （ 4~6 个）、 （ 7 个及以上），以下是根据调查结果绘制的统计图的一部分．

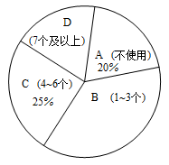
(1) 本次调查的样本容量是 _____ ，请补全条形统计图；

(2) 已知该小区有 1500 户家庭，调查小组估计：该小区 1 周内使用 7 个及以上环保塑料袋的家庭约有 225 户．调查小组的估计是否合理？请说明理由．

在 5 张相同的小纸条上，分别写有语句： ① 函数表达式为 ； ② 函数表达式为 ； ③ 函数的图像关于原点对称； ④ 函数的图像关于 轴对称； ⑤ 函数值 随自变量 增大而增大．将这 5 张小纸条做成 5 支签， ① 、 ② 放在不透明的盒子 中搅匀， ③ 、 ④ 、 ⑤ 放在不透明的盒子 中搅匀．

(1) 从盒子 中任意抽出 1 支签，抽到 ① 的概率是 ______ ；

(2) 先从盒子 中任意抽出 1 支签，再从盒子 中任意抽出 1 支签．求抽到的 2 张小纸条上的语句对函数的描述相符合的概率．

如图，在平面直角坐标系 中，一次函数 的图象分别与 轴、 轴交于点 、 ，与反比例函数 的图象交于点 ，连接 ．已知点 ， 的面积是 2 ．

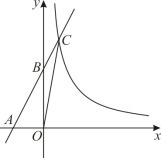
(1) 求 、 的值；

(2) 求 的面积．

如图，点 在射线 上， ．如果 绕点 按逆时针方向旋转 到 ，那么点 的位置可以用 表示．

(1) 按上述表示方法，若 ， ，则点 的位置可以表示为 ______ ；

(2) 在（ 1 ）的条件下，已知点 的位置用 表示，连接 、 ．求证： ．

第十四届国际数学教育大会（ ICME -14 ）会徽的主题图案有着丰富的数学元素，展现了我国古代数学的文化魅力，其右下方的 “ 卦 ” 是用我国古代的计数符号写出的八进制数 3745 ．八进制是以 8 作为进位基数的数字系统，有 0~7 共 8 个基本数字．八进制数 3745 换算成十进制数是 ，表示 ICME -14 的举办年份．

(1) 八进制数 3746 换算成十进制数是 _______ ；

(2) 小华设计了一个 进制数 143 ，换算成十进制数是 120 ，求 的值．

在四边形 中， 是边 上的一点．若 ，则点 叫做该四边形的 “ 等形点 ” ．

(1) 正方形 _______“ 等形点 ” （填 “ 存在 ” 或 “ 不存在 ” ）；

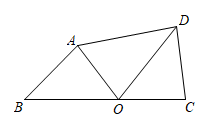
(2) 如图，在四边形 中，边 上的点 是四边形 的 “ 等形点 ” ．已知 ， ， ，连接 ，求 的长；

(3) 在四边形 中， EH // FG ．若边 上的点 是四边形 的 “ 等形点 ” ，求 的值．

已知二次函数 的自变量 的部分取值和对应函数值 如下表：

(1) 求二次函数 的表达式；

(2) 将二次函数 的图像向右平移 个单位，得到二次函数 的图像，使得当 时， 随 增大而增大；当 时， 随 增大而减小，请写出一个符合条件的二次函数 的表达式 ______ ，实数 的取值范围是 _______ ；

(3) 、 、 是二次函数 的图像上互不重合的三点．已知点 、 的横坐标分别是 、 ，点 与点 关于该函数图像的对称轴对称，求 的度数．

（现有若干张相同的半圆形纸片，点 是圆心，直径 的长是 ， 是半圆弧上的一点（点 与点 、 不重合），连接 、 ．

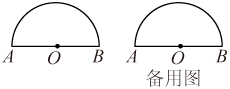
(1) 沿 、 剪下 ，则 是 ______ 三角形（填 “ 锐角 ” 、 “ 直角 ” 或 “ 钝角 ” ）；

(2) 分别取半圆弧上的点 、 和直径 上的点 、 ．已知剪下的由这四个点顺次连接构成的四边形是一个边长为 的菱形．请用直尺和圆规在图中作出一个符合条件的菱形（保留作图痕迹，不要求写作法）；

(3) 经过数次探索，小明猜想，对于半圆弧上的任意一点 ，一定存在线段 上的点 、线段 上的点 和直径 上的点 、 ，使得由这四个点顺次连接构成的四边形是一个边长为 的菱形．小明的猜想是否正确？请说明理由．