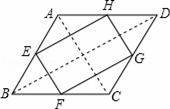
依次连接菱形的四边中点得到的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.三角形
A【考点】中点四边形.
【分析】作出图形,根据三角形的中位线平行于第三边并且等于第三边的一半判定出四边形EFGH是平行四边形,再根据菱形的对角线互相垂直可得EF⊥FG,然后根据有一个角是直角的平行四边形是矩形判断.
【解答】解:如图,∵E、F分别是AB、BC的中点,
∴EF∥AC且EF=![]()
![]() AC,
AC,
同理,GH∥AC且GH=![]()
![]() AC,
AC,
∴EF∥GH且EF=GH,
∴四边形EFGH是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
又根据三角形的中位线定理,EF∥AC,FG∥BD,
∴EF⊥FG,
∴平行四边形EFGH是矩形.
故选A.

【点评】本题主要考查了三角形的中位线定理,菱形的性质,以及矩形的判定,连接四边形的中点得到的四边形的形状主要与原四边形的对角线的关系有关,原四边形的对角线相等,则得到的四边形是菱形,原四边形对角线互相垂直,则得到的四边形是矩形,连接任意四边形的四条边的中点得到的四边形都是平行四边形.
是一种平面图形,矩形的四个角都是直角,同时矩形的对角线相等,而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。
2、矩形的性质:(1)具有平行四边形的一切性质
(2)矩形的四个角都是直角
(3)矩形的对角线相等
(4)矩形是轴对称图形,也是中心对称图形。
3、矩形的判定:(1)定义:有一个角是直角的平行四边形是矩形
(2)定理1:有三个角是直角的四边形是矩形
(3)定理2:对角线相等的平行四边形是矩形
4、矩形的面积:S矩形=长×宽=ab。
矩形的性质:
1.矩形的4个内角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴。对称中心是对角线的交点。
5.矩形是特殊的平行四边形,矩形具有平行四边形的所有性质
6.顺次连接矩形各边中点得到的四边形是菱形
①定义:有一个角是直角的平行四边形是矩形
②定理1:有三个角是直角的四边形是矩形
③定理2:对角线相等的平行四边形是矩形
④对角线互相平分且相等的四边形是矩形
矩形的面积:S矩形=长×宽=ab。
宽与长的比是(√5-1)/2(约为0.618)的矩形叫做黄金矩形。
黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。如希腊的巴特农神庙等。
2、经历探索、猜测、证明的过程,发展学生的推理论证能力。
3、通过独立完成证明的过程,体会数学是严谨的科学,增强学生对待科学的严谨治学态度,从而养成良好的习惯。
课时要求:130
考试频率:常考
分值比重:7