在下列图形中,既是轴对称图形又是中心对称图形的是( )
A . 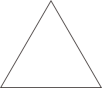 B .
B . 
C . 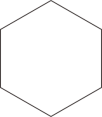 D .
D . 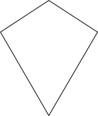
下列计算正确的是( )
A . B .
C .
D .
函数 中,自变量 x 的取值范围是( )
A . B .
C .
D .
由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是( )

A . 3 B . 4 C . 5 D . 6
不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )
A . B .
C .
D .
如图, BD 是 的直径, A , C 在圆上,
,
的度数是( )
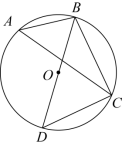
A . 50° B . 45° C . 40° D . 35°
如图,等边三角形 OAB ,点 B 在 x 轴正半轴上, ,若反比例函数
图象的一支经过点 A ,则 k 的值是( )
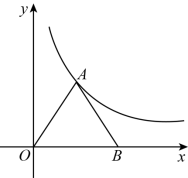
A . B .
C .
D .
若关于 x 的方程 无解,则 m 的值为( )
A . 1 B . 1 或 3 C . 1 或 2 D . 2 或 3
圆锥的底面圆半径是 1 ,母线长是 3 ,它的侧面展开图的圆心角是( )
A . 90° B . 100° C . 120° D . 150°
观察下列数据: ,
,
,
,
, … ,则第 12 个数是( )
A . B .
C .
D .
下列图形是黄金矩形的折叠过程:第一步,如图( 1 ),在一张矩形纸片一端折出一个正方形,然后把纸片展平;第二步,如图( 2 ),把正方形折成两个相等的矩形再把纸片展平;第三步,折出内侧矩形的对角线 AB ,并把 AB 折到图( 3 )中所示的 AD 处;第四步,如图( 4 ),展平纸片,折出矩形 BCDE 就是黄金矩形.则下列线段的比中: ① , ②
, ③
, ④
,比值为
的是( )
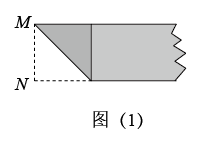
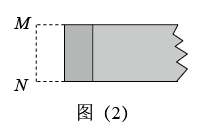
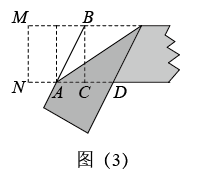
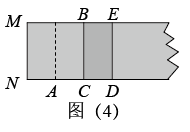
A . ①② B . ①③ C . ②④ D . ②③
如图,抛物线 的对称轴是
,并与 x 轴交于 A , B 两点,若
,则下列结论中: ①
; ②
; ③
; ④ 若 m 为任意实数,则
,正确的个数是( )
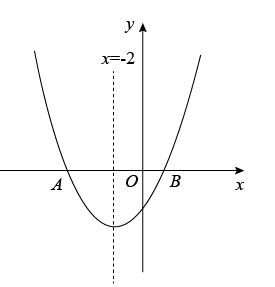
A . 1 B . 2 C . 3 D . 4
在 2022 年 3 月 13 日北京冬残奥会闭幕当天,奥林匹克官方旗舰店再次发售 1000000 只 “ 冰墩墩 ” ,很快便售罄.数据 1000000 用科学记数法表示为 .
如图, ,
,请添加一个条件 ,使
.
某商品的进价为每件 10 元,若按标价打八折售出后,每件可获利 2 元,则该商品的标价为每件 元.
一列数据: 1 , 2 , 3 , x , 5 , 5 的平均数是 4 ,则这组数据的中位数是 .
的直径
, AB 是
的弦,
,垂足为 M ,
,则 AC 的长为 .
抛物线 向右平移 2 个单位长度,再向上平移 3 个单位长度,得到抛物线的顶点坐标是 .
如图,在平面直角坐标系中,点 ,
,将平行四边形 OABC 绕点 O 旋转 90° 后,点 B 的对应点
坐标是 ______ .

如图,在等腰直角三角形 ABC 和等腰直角三角形 ADE 中, ,点 D 在 BC 边上, DE 与 AC 相交于点 F ,
,垂足是 G ,交 BC 于点 H .下列结论中: ①
; ②
; ③ 若
,
,则
; ④
,正确的是 ______ .

先化简,再求值. ,其中
.
已知抛物线 与 x 轴交于
,
两点,与 y 轴交于点 C ,顶点为 D .

(1) 求该抛物线的解析式;
(2) 连接 BC , CD , BD , P 为 BD 的中点,连接 CP ,则线段 CP 的长是 ______ .注:抛物线 的对称轴是直线
,顶点坐标是
.
在菱形 ABCD 中,对角线 AC 和 BD 的长分别是 6 和 8 ,以 AD 为直角边向菱形外作等腰直角三角形 ADE .连接 CE .请用尺规或三角板作出图形,并直接写出线段 CE 的长.
为推进 “ 冰雪进校园 ” 活动,我市某初级中学开展: A .速度滑冰, B .冰尜, C .雪地足球, D .冰壶, E .冰球等五种冰雪体育活动,并在全校范围内随机抽取了若干名学生,对他们最喜爱的冰雪体育活动的人数进行统计(要求:每名被抽查的学生必选且只能选择一种),绘制了如图所示的条形统计图和扇形统计图.

请解答下列问题:
(1) 这次被抽查的学生有多少人?
(2) 请补全条形统计图,并写出扇形统计图中 B 类活动扇形圆心角的度数是 ______ ;
(3) 若该校共有 1500 人,请你估计全校最喜爱雪地足球的学生有多少人?
在一条平坦笔直的道路上依次有 A , B , C 三地,甲从 B 地骑电瓶车到 C 地,同时乙从 B 地骑摩托车到 A 地,到达 A 地后因故停留 1 分钟,然后立即掉头(掉头时间忽略不计)按原路原速前往 C 地,结果乙比甲早 2 分钟到达 C 地,两人均匀速运动,如图是两人距 B 地路程 y (米)与时间 x (分钟)之间的函数图象.

请解答下列问题:
(1) 填空:甲的速度为 ______ 米 / 分钟,乙的速度为 ______ 米 / 分钟;
(2) 求图象中线段 FG 所在直线表示的 y (米)与时间 x (分钟)之间的函数解析式,并写出自变量 x 的取值范围;
(3) 出发多少分钟后,甲乙两人之间的路程相距 600 米?请直接写出答案.
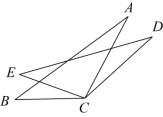
如图, 和
,点 E , F 在直线 BC 上,
,
,
.如图 ① ,易证:
.请解答下列问题:


(1) 如图 ② ,如图 ③ ,请猜想 BC , BE , BF 之间的数量关系,并直接写出猜想结论;
(2) 请选择( 1 )中任意一种结论进行证明;
(3) 若 ,
,
,
,则
______ ,
______ .
某工厂准备生产 A 和 B 两种防疫用品,已知 A 种防疫用品每箱成本比 B 种防疫用品每箱成本多 500 元.经计算,用 6000 元生产 A 种防疫用品的箱数与用 4500 元生产 B 种防疫用品的箱数相等.请解答下列问题:
(1) 求 A , B 两种防疫用品每箱的成本;
(2) 该工厂计划用不超过 90000 元同时生产 A 和 B 两种防疫用品共 50 箱,且 B 种防疫用品不超过 25 箱,该工厂有几种生产方案?
(3) 为扩大生产,厂家欲拿出与( 2 )中最低成本相同的费用全部用于购进甲和乙两种设备(两种都买).若甲种设备每台 2500 元,乙种设备每台 3500 元,则有几种购买方案?最多可购买甲,乙两种设备共多少台?(请直接写出答案即可)
