据测算,世博会召开时,上海使用清洁能源可减少二氧化碳排放约 16 万吨,将 16 万吨用科学记数法表示为( )
A . 吨 B .
吨 C .
吨 D .
吨
下列图形中是轴对称图形但不是中心对称图形的是( )
A .  B .
B .  C .
C .  D .
D . ![]()
左下图是一些完全相同的小正方体搭成的几何体的三视图 .这个几何体只能是( )
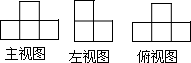
A . ![]() B .
B . ![]() C .
C . ![]() D .
D . ![]()
一组数据 13 , 10 , 10 , 11 , 16 的中位数和平均数分别是( )
A . 11 , 13 B . 11 , 12 C . 13 , 12 D . 10 , 12
下列方程没有实数根的是( )
A . B .
C . D .
若二次函数 的图象经过点 P (- 2 , 4 ),则该图象必经过点( )
A .( 2 , 4 ) B .(- 2 ,- 4 ) C .(- 4 , 2 ) D .( 4 ,- 2 )
函数 自变量 x 的取值范围是【 】
A . x≥1 且 x≠3 B . x≥1 C . x≠3 D . x > 1 且 x≠3
王老师对本班 40 名学生的血型作了统计,列出如下的统计表,则本班 A 型血的人数是()
| 组别 | A 型 | B 型 | AB 型 | O 型 |
| 频率 | 0.4 | 0.35 | 0.1 | 0.15 |
A . 16 人 B . 14 人 C . 4 人 D . 6 人
袋子里有 4 个球 , 标有 2,3,4,5, 先抽取一个并记住 , 放回 , 然后再抽取一个 , 所抽取的两个球数字之和大于 6 的概率是 ( )
A . B .
C .
D .
小明去爬山,在山脚看山顶角度为 30° ,小明在坡比为 5∶12 的山坡上走 1300 米,此时小明看山顶的角度为 60° ,求山高 ( )
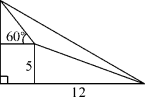
A . (600 - 250 ) 米 B . (600
- 250) 米
C . (350 + 350 ) 米 D . 500
米
分解因式: .
若两个连续的整数 、
满足
,则
的值为 .
已知圆锥的高是 12 ,底面圆的半径为 5 ,则这个圆锥的侧面展开图的周长为
在九张质地都相同的卡片上分别写有数字﹣ 4 ,﹣ 3 ,﹣ 2 ,﹣ 1 , 0 , 1 , 2 , 3 , 4 ,从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于 2 的概率是 .
把二次函数 y=2x 2 的图象向左平移 1 个单位长度,再向下平移 2 个单位长度,平移后抛物线的解析式为 .
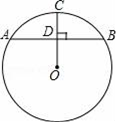
如图,在 ⊙O 中,弦 AB 垂直平分半径 OC ,垂足为 D ,若 ⊙O 的半径为 2 ,则弦 AB 的长为 .
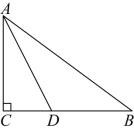
在 Rt△ABC 中, ∠C=90° , AD 平分 ∠CAB , AC=6 , BC=8 , CD= .
如图所示,以 O 为端点画六条射线后 OA , OB , OC , OD , OE , O 后 F ,再从射线 OA 上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8… 后,那么所描的第 2013 个点在射线 上.
某玩具厂生产一种玩具,甲车间计划生产 500 个,乙车间计划生产 400 个,甲车间每天比乙车间多生产 10 个,两车间同时开始生产且同时完成任务 .设乙车间每天生产 个,可列方程为 .
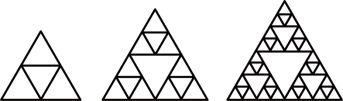
下列图形是将等边三角形按一定规律排列,则第 个图形中所以等边三角形的个数是 .
先化简,再求值: ,在﹣ 2 , 0 , 1 , 2 四个数中选一个合适的代入求值.
如图,在边长为 1 个单位长度的小正方形组成的网格中, △ ABC 与 △ DEF 关于点 O 成中心对称, △ ABC 与 △ DEF 的顶点均在格点上,请按要求完成下列各题.
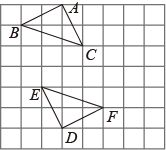
( 1 )在图中画出点 O 的位置;
( 2 )将 △ ABC 先向右平移 4 个单位长度,再向下平移 2 个单位长度,得到 △ A 1 B 1 C 1 ,请画出 △ A 1 B 1 C 1 ;
( 3 )在网格中画出格点 M ,使 A 1 M 平分 ∠ B 1 A 1 C 1
如图,已知抛物线 ( a > 0 )与 x 轴交于点 B 、 C ,与 y 轴交于点 E ,且点 B 在点 C 的左侧.
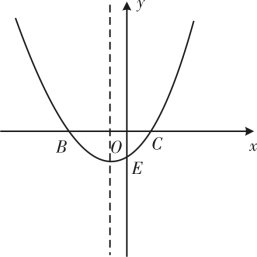
( 1 )若抛物线过点 M (﹣ 2 ,﹣ 2 ),求实数 a 的值;
( 2 )在( 1 )的条件下,解答下列问题;
① 求出 △ BCE 的面积;
② 在抛物线的对称轴上找一点 H ,使 CH + EH 的值最小,直接写出点 H 的坐标.
某电视台为了解观众对 “ 谍战 ” 题材电视剧的喜爱情况,随机抽取某社区部分电视观众,进行问卷调查,整理绘制了如下不完整的条形统计图和扇形统计图:
男、女观众对 “ 谍战 ” 题材电视剧的喜爱情况统计图
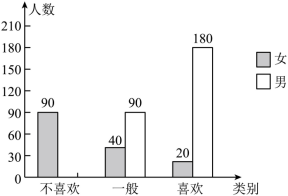
男观众对 “ 谍战 ” 题材电视剧的喜爱情况统计图
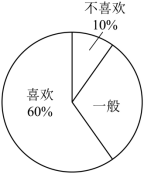
请根据以上信息,解答下列问题:
(1) 在这次接受调查的女观众中,表示 “ 不喜欢 ” 的女观众所占的百分比是多少?
(2) 求这次调查的男观众人数,并补全条形统计图.
(3) 若该社区有男观众约 1000 人,估计该社区男观众喜欢看 “ 谍战 ” 题材电视剧的约有多少人?
2008 年 5 月 12 日 14 时 28 分四川汶川发生里氏 8.0 级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点 480 千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发 1.25 小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程 y 甲 (千米)、 y 乙 (千米)与时间 x (小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
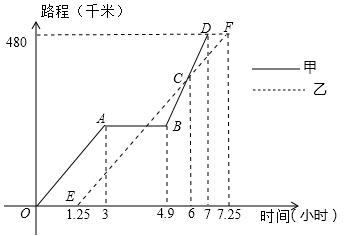
(1) 由于汽车发生故障,甲组在途中停留了 小时;
(2) 甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3) 为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过 25 千米,请通过计算说明,按图象所表示的走法是否符合约定?
在菱形 和正三角形
中,
,
是
的中点,连接
、
.
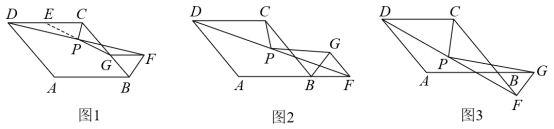
(1) 如图 1 ,当点 在
边上时,写出
与
的数量关系 .(不必证明)
(2) 如图 2 ,当点 在
的延长线上时,线段
、
有怎样的数量关系,写出你的猜想,并给予证明;
(3) 如图 3 ,当点 在
的延长线上时,线段
、
又有怎样的数量关系,写出你的猜想(不必证明).
为了迎接 “ 十 • 一 ” 小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
| 运动鞋 价格 | 甲 | 乙 |
| 进价(元 / 双) | m | m ﹣ 20 |
| 售价(元 / 双) | 240 | 160 |
已知:用 3000 元购进甲种运动鞋的数量与用 2400 元购进乙种运动鞋的数量相同.
( 1 )求 m 的值;
( 2 )要使购进的甲、乙两种运动鞋共 200 双的总利润(利润 = 售价﹣进价)不少于 21700 元,且不超过 22300 元,问该专卖店有几种进货方案?
( 3 )在( 2 )的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠 a ( 50 < a < 70 )元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
如图,直线 MN 与 x 轴, y 轴分别相交于 A , C 两点,分别过 A , C 两点作 x 轴, y 轴的垂线相交于 B 点,且 OA , OC ( OA > OC )的长分别是一元二次方程 x 2 ﹣ 14x+48=0 的两个实数根.
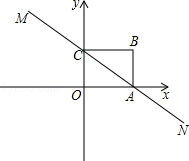
( 1 )求 C 点坐标;
( 2 )求直线 MN 的解析式;
( 3 )在直线 MN 上存在点 P ,使以点 P , B , C 三点为顶点的三角形是等腰三角形,请直接写出 P 点的坐标.