的倒数是( )
A . B .
C .
D .
地球上的陆地面积约为 ,数字
用科学记数法表示为 ( )
A . B .
C .
D .
实数 c , d 在数轴上的对应点如图所示,则下列式子正确的是 ( )
![]()
A . B .
C .
D .
下列图形中,既是轴对称图形又是中心对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
小明同学对数据 12 , 22 , 36 , 4■ , 52 进行统计分析,发现其中一个两位数的个位数字被墨水污染已无法看清,则下列统计量与被污染数字无关的是 ( )
A .平均数 B .标准差 C .方差 D .中位数
已知圆锥的底面半径为 5 ,高为 12 ,则它的侧面展开图的面积是 ( )
A . B .
C .
D .
如图,将平行四边形 沿对角线
折叠,使点 A 落在 E 处.若
,
,则
的度数为 ( )
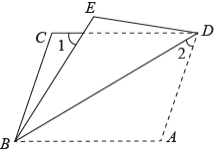
A . B .
C .
D .
下列说法 不正确 的是 ( )
A .有两个角是锐角的三角形是直角或钝角三角形
B .有两条边上的高相等的三角形是等腰三角形
C .有两个角互余的三角形是直角三角形
D .底和腰相等的等腰三角形是等边三角形
平面直角坐标系中,点 M 在 y 轴的非负半轴上运动,点 N 在 x 轴上运动,满足 .点 Q 为线段
的中点,则点 Q 运动路径的长为 ( )
A . B .
C .
D .
函数 叫做高斯函数,其中 x 为任意实数,
表示不超过 x 的最大整数.定义
,则下列说法正确的个数为 ( )
① ;
② ;
③ 高斯函数 中,当
时, x 的取值范围是
;
④ 函数 中,当
时,
.
A . 0 B . 1 C . 2 D . 3
在函数 中,自变量
的取值范围是 .
写出一个过点 且 y 随 x 增大而减小的一次函数关系式 .
满足不等式组 的整数解是 .
不透明的盒中装有三张卡片,编号分别为 1 , 2 , 3 .三张卡片质地均匀,大小、形状完全相同,摇匀后从中随机抽取一张卡片记下编号,然后放回盒中再摇匀,再从盒中随机取出一张卡片,则两次所取卡片的编号之积为奇数的概率为 .
已知代数式 是一个完全平方式,则实数 t 的值为 .
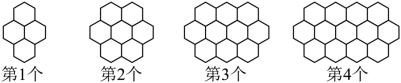
观察下列 “ 蜂窝图 ” ,按照这样的规律,则第 16 个图案中的 “ ![]() ” 的个数是 .
” 的个数是 .
已知函数 的图象与坐标轴恰有两个公共点,则实数 m 的值为 .
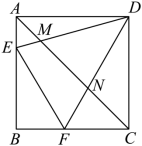
如图,正方形 中,点 E , F 分别是边
上的两个动点,且正方形
的周长是
周长的 2 倍,连接
分别与对角线
交于点 M , N .给出如下几个结论: ① 若
,则
; ②
; ③ 若
,则
; ④ 若
,则
.其中正确结论的序号为 .
计算: .
先化简,再求值: .其中
.
某工厂生产某种零件,由于技术上的改进,现在平均每天比原计划多生产 20 个零件,现在生产 800 个零件所需时间与原计划生产 600 个零件所需时间相同.求现在平均每天生产多少个零件?
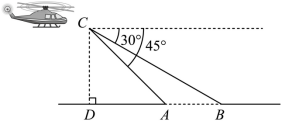
如图,为了修建跨江大桥,需要利用数学方法测量江的宽度 .飞机上的测量人员在 C 处测得 A , B 两点的俯角分别为
和
.若飞机离地面的高度
为
,且点 D , A , B 在同一水平直线上,试求这条江的宽度
(结果精确到
,参考数据:
)
中华文化源远流长,中华诗词寓意深广,为了传承优秀传统文化,我市某校团委组织了一次全校 2000 名学生参加的 “ 中国诗词大会 ” 海选比赛,赛后发现所有参赛学生的成绩不低于 50 分,为了更好地了解本次海选比赛的成绩分布情况.随机选取其中 200 名学生的海选比赛成绩(总分 100 分)作为样本进行整理,得到海选成绩统计表与扇形统计图如下:
抽取的 200 名学生成绩统计表
| 组别 | 海选成绩 | 人数 |
| A 组 | | 10 |
| B 组 | | 30 |
| C 组 | | 40 |
| D 组 | | a |
| E 组 | | 70 |
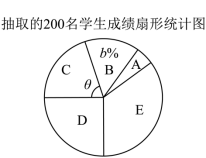 请根据所给信息解答下列问题:
请根据所给信息解答下列问题:
(1) 填空: ① ____________ , ②
____________ , ③
____________ 度;
(2) 若把统计表每组中各个成绩用这组数据的中间值代替(例如: A 组数据中间值为 55 分),请估计被选取的 200 名学生成绩的平均数;
(3) 规定海选成绩不低于 90 分记为 “ 优秀 ” ,请估计该校参加这次海选比赛的 2000 名学生中成绩 “ 优秀 ” 的有多少人?
如图,在四边形 中,点 E , C 为对角线
上的两点,
.连接
.
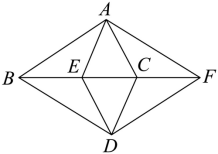
(1) 求证:四边形 是平行四边形;
(2) 若 ,求证:
.
已知反比例函数 和一次函数
,其中一次函数图象过
,
两点.
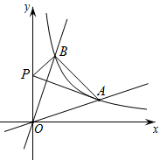
(1) 求反比例函数的关系式;
(2) 如图,函数 的图象分别与函数
图象交于 A , B 两点,在 y 轴上是否存在点 P ,使得
周长最小?若存在,求出周长的最小值;若不存在,请说明理由.
果园有果树 60 棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种 10 棵果树时,果园内的每棵果树平均产量为 .在确保每棵果树平均产量不低于
的前提下,设增种果树 x (
且 x 为整数)棵,该果园每棵果树平均产量为
,它们之间的函数关系满足如图所示的图象.
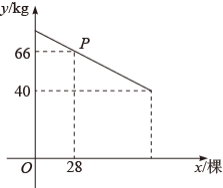
(1) 图中点 P 所表示的实际意义是 ________________________ ,每增种 1 棵果树时,每棵果树平均产量减少 ____________ ;
(2) 求 y 与 x 之间的函数关系式,并直接写出自变量 x 的取值范围;
(3) 当增种果树多少棵时,果园的总产量 最大?最大产量是多少?
如图,已知 是
外接圆
的直径,
.点 D 为
外的一点,
.点 E 为
中点,弦
过点 E .
.连接
.
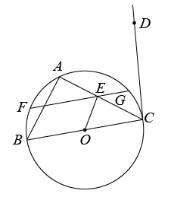
(1) 求证: 是
的切线;
(2) 求证: ;
(3) 当 时,求弦
的长.
已知二次函数 图像的对称轴为直线
.将二次函数
图像中 y 轴左侧部分沿 x 轴翻折,保留其他部分得到新的图像 C .
(1) 求 b 的值;
(2)① 当 时,图像 C 与 x 轴交于点 M , N ( M 在 N 的左侧),与 y 轴交于点 P .当
为直角三角形时,求 m 的值;
② 在 ① 的条件下,当图像 C 中 时,结合图像求 x 的取值范围;
(3) 已知两点 ,当线段
与图像 C 恰有两个公共点时,直接写出 m 的取值范围.