下列运算中,计算正确的是( )
A . B .
C . D .
下列图形是汽车的标识,其中是中心对称图形但不是轴对称图形的是( )
A .  B .
B . 
C .  D .
D . 
学校举办跳绳比赛,九年( 2 )班参加比赛的 6 名同学每分钟跳绳次数分别是 172 , 169 , 180 , 182 , 175 , 176 ,这 6 个数据的中位数是( )
A . 181 B . 175 C . 176 D . 175.5
如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是( )
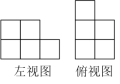
A . 7 B . 8 C . 9 D . 10
2022 年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了 45 场,共有多少支队伍参加比赛?( )
A . 8 B . 10 C . 7 D . 9
已知关于 x 的分式方程 的解是正数,则 m 的取值范围是( )
A . B .
C .
且
D .
且
国家 “ 双减 ” 政策实施后,某校开展了丰富多彩的社团活动.某班同学报名参加书法和围棋两个社团,班长为参加社团的同学去商场购买毛笔和围棋(两种都购买)共花费 360 元.其中毛笔每支 15 元,围棋每副 20 元,共有多少种购买方案?( )
A . 5 B . 6 C . 7 D . 8
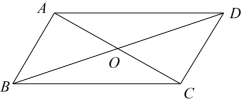
如图,在平面直角坐标系中,平行四边形 ABCD 的边 AB 在 x 轴上,顶点 D 在 y 轴的正半轴上, M 为 BC 的中点, OA 、 OB 的长分别是一元二次方程 的两个根
,
,动点 P 从点 D 出发以每秒 1 个单位长度的速度沿折线
向点 B 运动,到达 B 点停止.设运动时间为 t 秒,
的面积为 S .
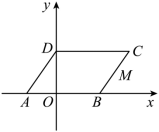
(1) 求点 C 的坐标;
(2) 求 S 关于 t 的函数关系式,并写出自变量 t 的取值范围;
(3) 在点 P 的运动过程中,是否存在点 P ,使 是等腰三角形?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
如图, 中,
, AD 平分
与 BC 相交于点 D ,点 E 是 AB 的中点,点 F 是 DC 的中点,连接 EF 交 AD 于点 P .若
的面积是 24 ,
,则 PE 的长是( )
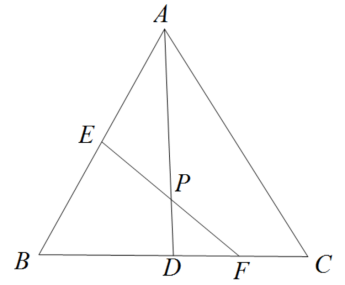
A . 2.5 B . 2 C . 3.5 D . 3
如图,正方形 ABCD 的对角线 AC , BD 相交于点 O ,点 F 是 CD 上一点, 交 BC 于点 E ,连接 AE , BF 交于点 P ,连接 OP .则下列结论: ①
; ②
; ③
; ④ 若
,则
; ⑤ 四边形 OECF 的面积是正方形 ABCD 面积的
.其中正确的结论是( )
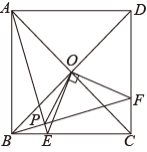
A . ①②④⑤ B . ①②③⑤ C . ①②③④ D . ①③④⑤
我国南水北调东线北延工程 2021-2022 年度供水任务顺利完成,共向黄河以北调水 1.89 亿立方米,将数据 1.89 亿用科学记数法表示为 .
函数 中自变量
的取值范围是 .
如图,在四边形 ABCD 中,对角线 AC , BD 相交于点 O , ,请你添加一个条件 ,使
.
在一个不透明的口袋中,有 2 个红球和 4 个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个球,摸到红球的概率是 .
若关于 x 的一元一次不等式组 的解集为
,则 a 的取值范围是 .
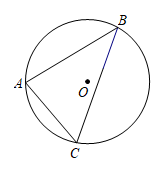
如图,在 中, AB 是
的弦,
的半径为 3cm , C 为
上一点,
,则 AB 的长为 cm .
若一个圆锥的母线长为 5cm ,它的侧面展开图的圆心角为 120° ,则这个圆锥的底面半径为 cm .
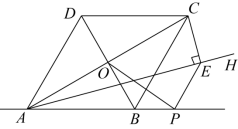
如图,菱形 ABCD 中,对角线 AC , BD 相交于点 O , ,
, AH 是
的平分线,
于点 E ,点 P 是直线 AB 上的一个动点,则
的最小值是 .
在矩形 ABCD 中, ,
,点 E 在边 CD 上,且
,点 P 是直线 BC 上的一个动点.若
是直角三角形,则 BP 的长为 .
如图,在平面直角坐标系中,平行四边形 ABCD 的边 AB 在 x 轴上,顶点 D 在 y 轴的正半轴上, M 为 BC 的中点, OA 、 OB 的长分别是一元二次方程 的两个根
,
,动点 P 从点 D 出发以每秒 1 个单位长度的速度沿折线
向点 B 运动,到达 B 点停止.设运动时间为 t 秒,
的面积为 S .

(1) 求点 C 的坐标;
(2) 求 S 关于 t 的函数关系式,并写出自变量 t 的取值范围;
(3) 在点 P 的运动过程中,是否存在点 P ,使 是等腰三角形?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
先化简,再求值: ,其中
.
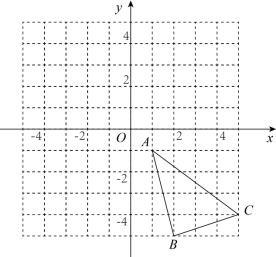
如图,在正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点坐标分别为
,
,
.
(1) 将 先向左平移 6 个单位,再向上平移 4 个单位,得到
,画出两次平移后的
,并写出点
的坐标;
(2) 画出 绕点
顺时针旋转 90° 后得到
,并写出点
的坐标;
(3) 在( 2 )的条件下,求点 旋转到点
的过程中所经过的路径长(结果保留
).
如图,抛物线 经过点
,点
,与 y 轴交于点 C ,抛物线的顶点为 D .
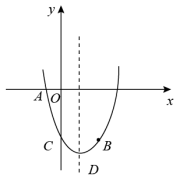
(1) 求抛物线的解析式;
(2) 抛物线上是否存在点 P ,使 的面积是
面积的 4 倍,若存在,请直接写出点 P 的坐标:若不存在,请说明理由.
为进一步开展 “ 睡眠管理 ” 工作,某校对部分学生的睡眠情况进行了问卷调查.设每名学生平均每天的睡眠时间为 x 小时,其中的分组情况是:
A 组: B 组:
C 组:
D 组:
E 组:
根据调查结果绘制成两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
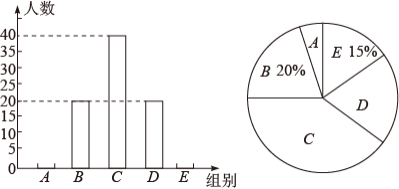
(1) 本次共调查了 _______ 名学生;
(2) 补全条形统计图;
(3) 在扇形统计图中,求 D 组所对应的扇形圆心角的度数;
(4) 若该校有 1500 名学生,请估计该校睡眠时间不足 9 小时的学生有多少人?
为抗击疫情,支援 B 市, A 市某蔬菜公司紧急调运两车蔬菜运往 B 市.甲、乙两辆货车从 A 市出发前往 B 市,乙车行驶途中发生故障原地维修,此时甲车刚好到达 B 市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往 B 市.乙车维修完毕后立即返回 A 市.两车离 A 市的距离 y ( km )与乙车所用时间 x ( h )之间的函数图象如图所示.
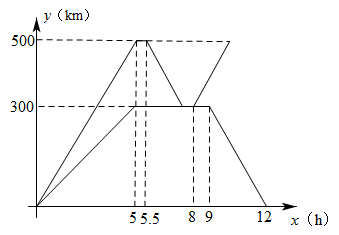
(1) 甲车速度是 _______km/h ,乙车出发时速度是 _______km/h ;
(2) 求乙车返回过程中,乙车离 A 市的距离 y ( km )与乙车所用时间 x ( h )的函数解析式(不要求写出自变量的取值范围);
(3) 乙车出发多少小时,两车之间的距离是 120km ?请直接写出答案.
和
都是等边三角形.
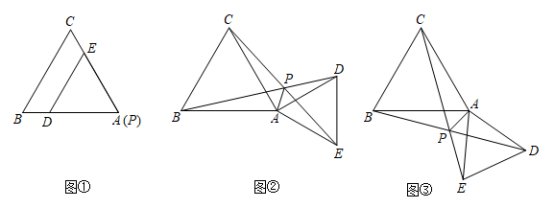
(1) 将 绕点 A 旋转到图 ① 的位置时,连接 BD , CE 并延长相交于点 P (点 P 与点 A 重合),有
(或
)成立;请证明.
(2) 将 绕点 A 旋转到图 ② 的位置时,连接 BD , CE 相交于点 P ,连接 PA ,猜想线段 PA 、 PB 、 PC 之间有怎样的数量关系?并加以证明;
(3) 将 绕点 A 旋转到图 ③ 的位置时,连接 BD , CE 相交于点 P ,连接 PA ,猜想线段 PA 、 PB 、 PC 之间有怎样的数量关系?直接写出结论,不需要证明.
学校开展大课间活动,某班需要购买 A 、 B 两种跳绳.已知购进 10 根 A 种跳绳和 5 根 B 种跳绳共需 175 元:购进 15 根 A 种跳绳和 10 根 B 种跳绳共需 300 元.
(1) 求购进一根 A 种跳绳和一根 B 种跳绳各需多少元?
(2) 设购买 A 种跳绳 m 根,若班级计划购买 A 、 B 两种跳绳共 45 根,所花费用不少于 548 元且不多于 560 元,则有哪几种购买方案?
(3) 在( 2 )的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?