﹣ 2022 的倒数是( )
A . 2022 B .﹣ C .﹣ 2022 D .
下面四个交通标志中,是中心对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
下列计算正确的是( )
A . B .
C . D .
数据 1 , 2 , 3 , 4 , 5 , x 存在唯一众数,且该组数据的平均数等于众数,则 x 的值为( )
A . 2 B . 3 C . 4 D . 5
由一些大小相同的小正方体搭成的几何体的主视图、左视图和俯视图都是如图所示的 “ 田 ” 字形,则搭成该几何体的小正方体的个数最少为( )

A . 4 个 B . 5 个 C . 6 个 D . 7 个
在单词 statistics ( 统计学 ) 中任意选择一个字母 , 字母为 “ s ” 的概率是( )
A . B .
C .
D .
如图所示,直线 a ∥ b ,点 A 在直线 a 上,点 B 在直线 b 上, AC = BC , ∠ C =120° , ∠1=43° ,则 ∠2 的度数为( )
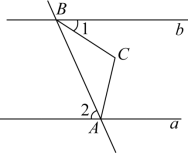
A . 57° B . 63°
C . 67° D . 73°
如图 ① 所示(图中各角均为直角 ) ,动点 Р 从点 A 出发,以每秒 1 个单位长度的速度沿 A → B → C → D → E 路线匀速运动, △ AFP 的面积 y 随点 Р 运动的时间 x (秒)之间的函数关系图象如图 ② 所示,下列说法正确的是( )
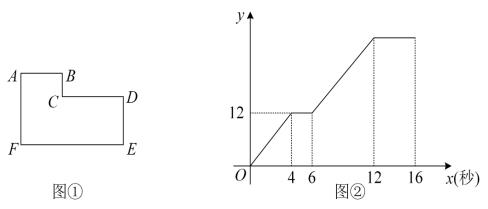
A . AF =5 B . AB =4 C . DE =3 D . EF =8
端午节前夕,某食品加工厂准备将生产的粽子装入 A 、 B 两种食品盒中, A 种食品盒每盒装 8 个粽子, B 种食品盒每盒装 10 个粽子,若现将 200 个粽子分别装入 A 、 B 两种食品盒中(两种食品盒均要使用并且装满),则不同的分装方式有( )
A . 2 种 B . 3 种 C . 4 种 D . 5 种
如图,二次函数
的图象与 y 轴的交点在( 0 , 1 )与( 0 , 2 )之间,对称轴为
,函数最大值为 4 ,结合图象给出下列结论: ①
; ②
; ③
; ④ 若关于 x 的一元二次方程
有两个不相等的实数根,则 m >4 ; ⑤ 当 x <0 时, y 随 x 的增大而减小.其中正确的结论有( )
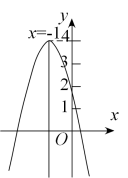
A . 2 个 B . 3 个 C . 4 个 D . 5 个
据统计, 2022 届高校毕业生规模预计首次突破千万,约为 10760000 人,总量和增量均为近年之最.将 10760000 用科学记数法表示为 .
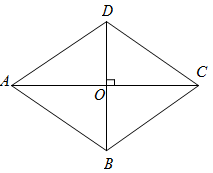
如图,在四边形 ABCD 中, AC ⊥ BD ,垂足为 O , ,要使四边形 ABCD 为菱形,应添加的条件是 .(只需写出一个条件即可)
已知圆锥的母线长为 高为
则该圆锥侧面展开图的圆心角是 .
若关于 x 的分式方程 的解大于 1 ,则 m 的取值范围是 .
如图,点 A 是反比例函数 图象上一点,过点 A 作 AB ⊥ y 轴于点 D ,且点 D 为线段 AB 的中点.若点 C 为 x 轴上任意一点,且 △ ABC 的面积为 4 ,则 k = .
在 △ ABC 中, ,
,
,则
.
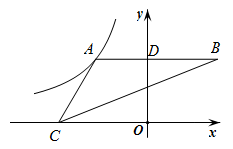
如图,直线 与
轴相交于点
,与
轴相交于点
,过点
作
交
轴于点
,过点
作
轴交
于点
,过点
作
交
轴于点
,过点
作
轴交
于点
… ,按照如此规律操作下去,则点
的纵坐标是 .
( 1 )计算 :
( 2 )因式分解:
解方程:
“ 双减 ” 政策实施后,某校为了解本校学生每天课后进行体育锻炼的时间情况,在 5 月份某天随机抽取了若干名学生进行调查,现将调查结果绘制成两幅尚不完整的统计图表.请根据统计图表提供的信息,回答下列问题:
| 组别 | 锻炼时间(分钟) | 频数(人) | 百分比 |
| A | | 50 | 25% |
| B | | m | 40% |
| C | | 40 | p |
| D | | n | 15% |
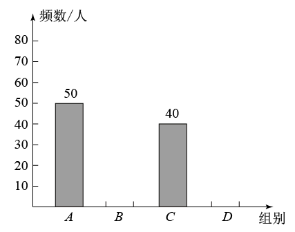 (1) 表中 m = , n = , p = ;
(1) 表中 m = , n = , p = ;
(2) 将条形图补充完整;
(3) 若制成扇形图,则 C 组所对应的圆心角为 ° ;
(4) 若该校学生有 2000 人,请根据以上调查结果估计:该校每天课后进行体育锻炼的时间超过 60 分钟的学生约有多少人 ?
如图,在 △ ABC 中, AB = AC ,以 AB 为直径作 ⊙ O , AC 与 ⊙ O 交于点 D , BC 与 ⊙ O 交于点 E ,过点 C 作 ,且 CF = CD ,连接 BF .
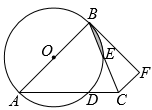
(1) 求证: BF 是 ⊙ O 的切线;
(2) 若 ∠ BAC =45° , AD =4 ,求图中阴影部分的面积.
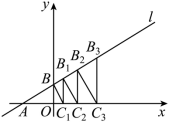
在一条笔直的公路上有 A 、 B 两地,甲、乙二人同时出发,甲从 A 地步行匀速前往 B 地,到达 B 地后,立刻以原速度沿原路返回 A 地.乙从 B 地步行匀速前往 A 地(甲、乙二人到达 A 地后均停止运动),甲、乙二人之间的距离 y (米)与出发时间 x (分钟)之间的函数关系如图所示,请结合图像解答下列问题:
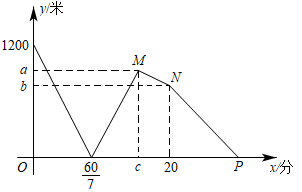
(1) A 、 B 两地之间的距离是 米,乙的步行速度是 米 / 分;
(2) 图中 a = , b = , c = ;
(3) 求线段 MN 的函数解析式;
(4) 在乙运动的过程中,何时两人相距 80 米 ? (直接写出答案即可)
综合与实践
数学是以数量关系和空间形式为主要研究对象的科学.数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系,让我们在学习与探索中发现数学的美,体会数学实践活动带给我们的乐趣.
如图 ① ,在矩形 ABCD 中,点 E 、 F 、 G 分别为边 BC 、 AB 、 AD 的中点,连接 EF 、 DF , H 为 DF 的中点,连接 GH .将 △ BEF 绕点 B 旋转,线段 DF 、 GH 和 CE 的位置和长度也随之变化.当 △ BEF 绕点 B 顺时针旋转 90° 时,请解决下列问题:
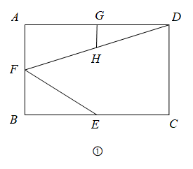
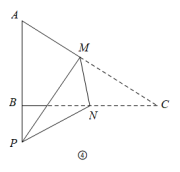
(1) 图 ② 中, AB = BC ,此时点 E 落在 AB 的延长线上,点 F 落在线段 BC 上,连接 AF ,猜想 GH 与 CE 之间的数量关系,并证明你的猜想;
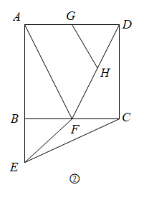
(2) 图 ③ 中, AB =2 , BC =3 ,则 ;
(3) 当 AB = m , BC = n 时. .
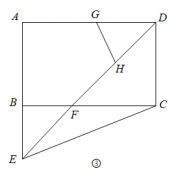
(4) 在( 2 )的条件下,连接图 ③ 中矩形的对角线 AC ,并沿对角线 AC 剪开,得 △ ABC (如图 ④) .点 M 、 N 分别在 AC 、 BC 上,连接 MN ,将 △ CMN 沿 MN 翻折,使点 C 的对应点 P 落在 AB 的延长线上,若 PM 平分 ∠ APN ,则 CM 长为 .
综合与探究
如图,某一次函数与二次函数 的图象交点为 A ( -1 , 0 ), B ( 4 , 5 ).
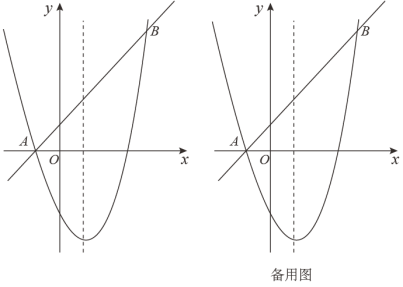
(1) 求抛物线的解析式;
(2) 点 C 为抛物线对称轴上一动点,当 AC 与 BC 的和最小时,点 C 的坐标为 ;
(3) 点 D 为抛物线位于线段 AB 下方图象上一动点,过点 D 作 DE ⊥ x 轴,交线段 AB 于点 E ,求线段 DE 长度的最大值;
(4) 在( 2 )条件下,点 M 为 y 轴上一点,点 F 为直线 AB 上一点,点 N 为平面直角坐标系内一点,若以点 C , M , F , N 为顶点的四边形是正方形,请直接写出点 N 的坐标.